Intervals for A, B and their difference.

Let \(\bar{A}\) be our estimator of the population mean \(\mu_A\) for Group A, and let \(\text{SE}(\bar{A})\) be its standard error. Similarly, let \(\bar{B}\) be our estimator of the population mean \(\mu_B\) for Group B, with standard error \(\text{SE}(\bar{B})\). If the samples we used to construct \(\bar{A}\) and \(\bar{B}\) are independent, then \(\text{Cov}(\bar{A}, \bar{B}) = 0\) and \[\text{SE}(\bar{A} - \bar{B}) = \sqrt{\text{SE}(\bar{A})^2 + \text{SE}(\bar{B})^2}\] as in the example from above. If \(\bar{A}\) and \(\bar{B}\) are approximately normally distributed, say by appealing to the central limit theorem, then we can construct 95% confidence intervals for \(\mu_A\), \(\mu_B\) as follows \[\mu_A \colon \quad \bar{A} \pm 2 \times \text{SE}(\bar{A}), \quad \quad \mu_B\colon \quad \bar{B} \pm 2 \times \text{SE}(\bar{B}).\] Similarly, we can construct a confidence interval for the difference in means \(\mu_A - \mu_B\), namely \[ (\bar{A} - \bar{B}) \pm 2 \times \text{SE}(\bar{A} - \bar{B}). \] More generally, to construct an approximate \((1 - \alpha) \times 100%\) confidence interval, we would replace the 2 above with the appropriate quantile of a standard normal distribution.¹ Below I’ll call this quantile \(z\) for short.

When is the difference significant?

The difference between \(\mu_A\) and \(\mu_B\) is statistically significant at the \(\alpha \times 100%\) level if the confidence interval for \(\Delta\) does not include zero, i.e. if \(|\bar{A} - \bar{B}| > z \cdot \text{SE}(\bar{A} - \bar{B})\). But working with absolute values will quickly become tedious, so without loss of generality, let’s assume \(\bar{A} \geq \bar{B}\). If this doesn’t hold, we can always relabel the two groups so it does hold. Then the condition for a significant difference becomes \[(\bar{A} - \bar{B})/z > \text{SE}(\bar{A} - \bar{B}).\]

When do the intervals overlap?

Again, without loss of generality, we can assume that \(\bar{A}\geq \bar{B}\). Now think about what it would mean for the two confidence intervals to overlap. The center of the interval for \(\mu_A\) is to the right of the center of the interval for \(\mu_B\) since \(\bar{A} \geq \bar{B}\). So for the two intervals to overlap, the lower confidence limit of the \(\mu_A\) interval must be to the left of the upper confidence limit of the \(\mu_B\) interval. This figure illustrates the logic using \(z = 2\).

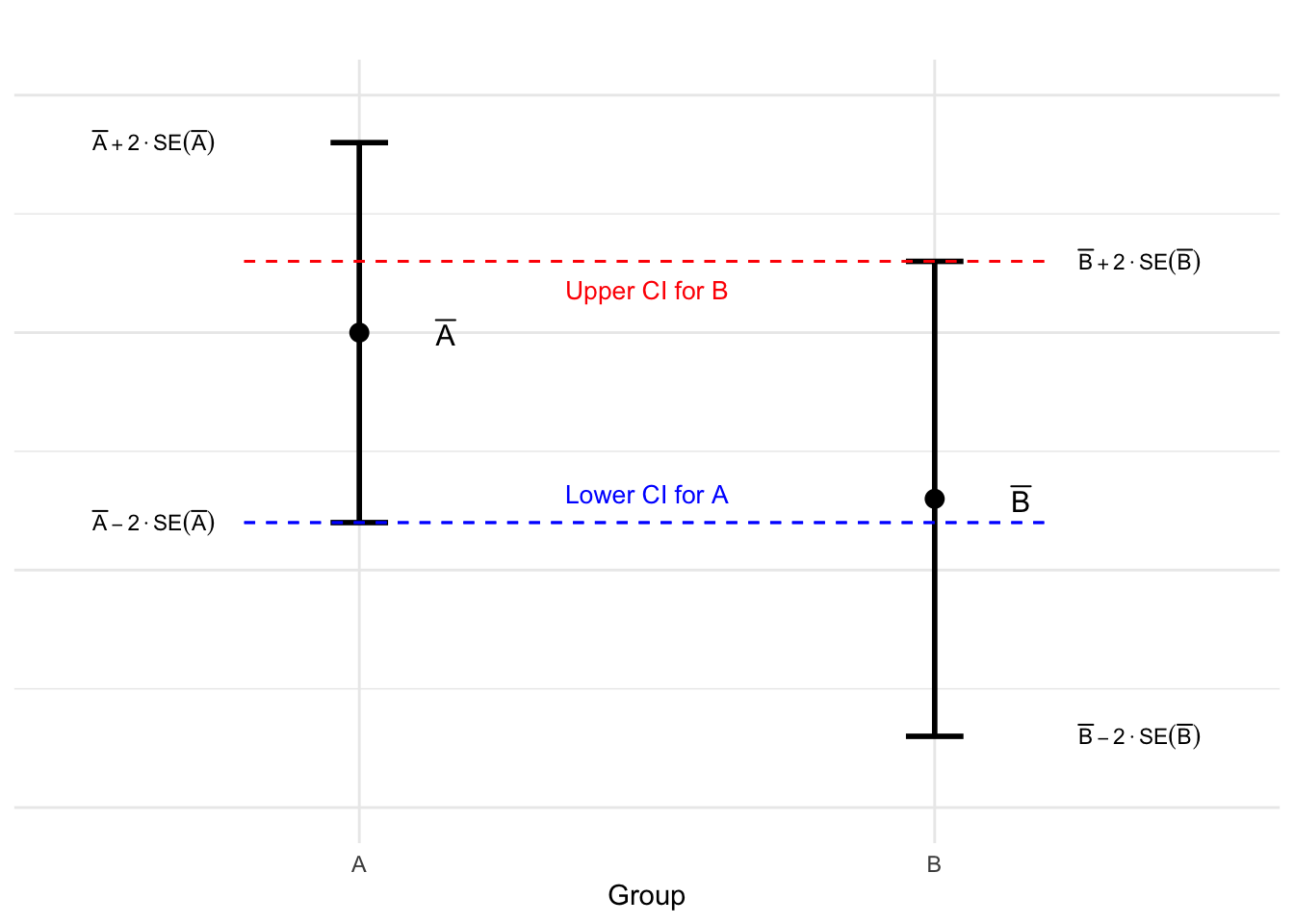
From the figure, we see that the two intervals overlap if \[\bar{A} - 2 \cdot \text{SE}(\bar{A}) < \bar{B} + 2 \cdot \text{SE}(\bar{B})\] Rearranging, and using the generic quantile \(z\), this becomes \[(\bar{A} - \bar{B})/z < \text{SE}(\bar{A}) + \text{SE}(\bar{B}).\]

Formalizing the Question

Can the confidence intervals for A and B overlap despite there being a significant difference of means between the two groups? Using the results from above, this question is equivalent to asking whether it’s possible for both of these inequalities to hold at the same time:

1. Overlapping CIs: \((\bar{A} - \bar{B})/z < \text{SE}(\bar{A}) + \text{SE}(\bar{B})\)
2. Significant Difference: \((\bar{A} - \bar{B})/z > \text{SE}(\bar{A} - \bar{B})\)

So the question becomes: can we find values of \(\bar{A}\), \(\bar{B}\), \(\text{SE}(\bar{A})\), and \(\text{SE}(\bar{B})\) such that \[\text{SE}(\bar{A} - \bar{B}) < \frac{\bar{A} - \bar{B}}{z} < \text{SE}(\bar{A}) + \text{SE}(\bar{B})?\]

Let’s talk about triangles!

For just a moment, forget that we’re talking about statistics and cast your mind back to high school geometry. There are two facts I’d like you to recall:

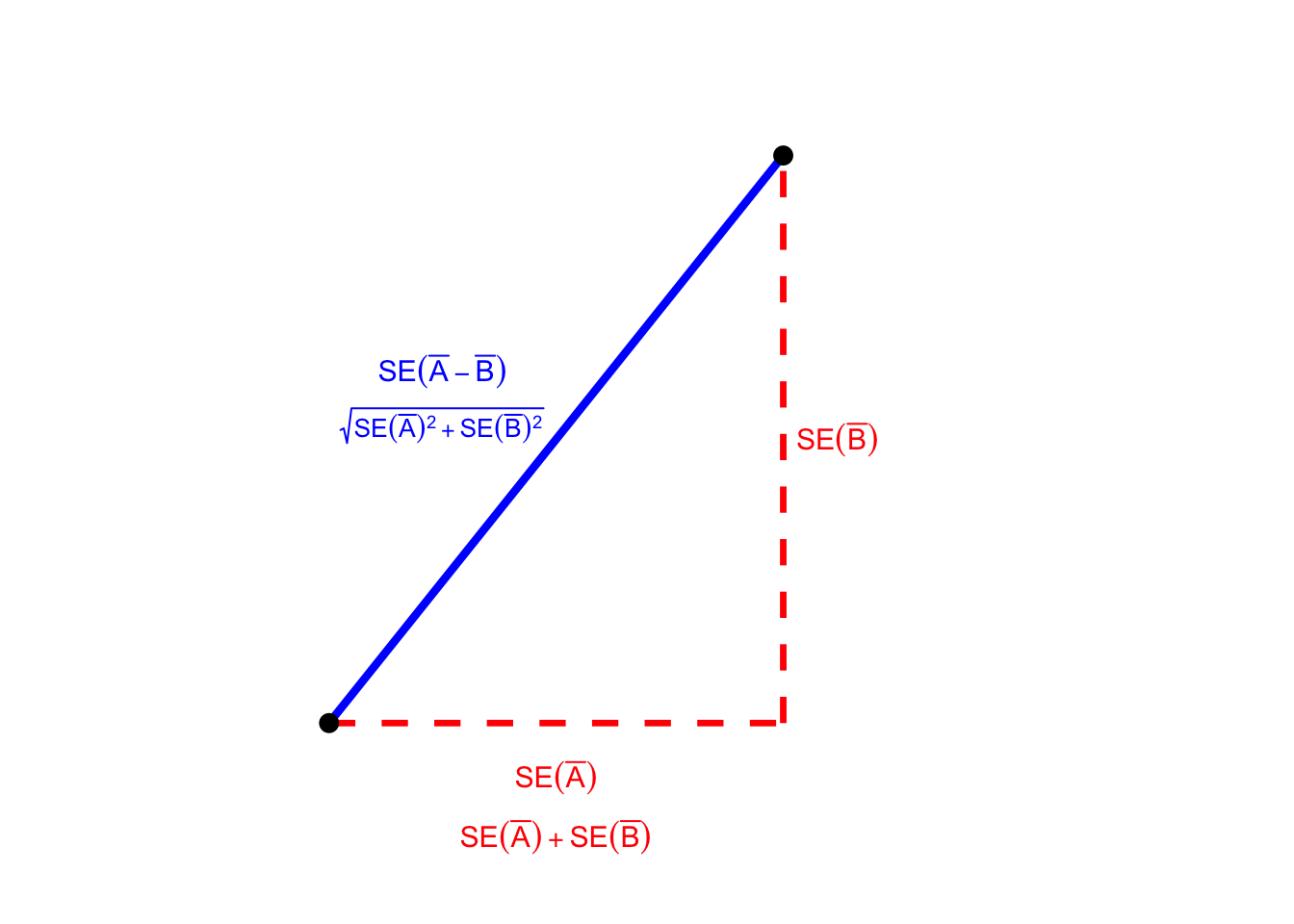
The Solution

The question we set out to answer is whether we can find values that satisfy the inequality: \[\text{SE}(\bar{A} - \bar{B}) < \frac{\bar{A} - \bar{B}}{z} < \text{SE}(\bar{A}) + \text{SE}(\bar{B}).\] Since the right-hand side is always strictly larger than the left-hand side, the answer is yes. Let’s try it out using a simple example. Suppose that \(\text{SE}(\bar{A}) = \text{SE}(\bar{B}) = 10\) as in the example from above, and consider a 95% confidence interval so that \(z \approx 2\). Then the inequality becomes \[ 20 \sqrt{2} < \bar{A} - \bar{B} < 40. \] Since \(20 \sqrt{2} \approx 28.28\) we have a whole range of values for \(\bar{A} - \bar{B}\) that will do the trick. For example, \(\bar{A}-\bar{B} = 30\) will do the trick. So if \(\text{SE}(\bar{A}) = \text{SE}(\bar{B}) = 10\), \(\bar{A} = 40\) and \(\bar{B} = 10\), the 95% CIs for A and B overlap but there is a significant difference between the two groups. This is the opposite of Gelman & Stern’s example.

Our inequality from above depends only the difference between \(\bar{A}\) and \(\bar{B}\), not on the individual value of each sample mean. So if we keep the same standard errors as before but set \(\bar{A} = 15\) and \(\bar{B} = -15\), so the difference of means remains 30, we obtain the same result: overlapping intervals with a significant difference between the two groups. Notice anything interesting about this example? The interval for A is \((-5,35)\) while the interval for B is \((-35, 5)\). So both intervals include zero but there is still a significant difference between them! If all we know is that two intervals overlap, we can’t say anything about the significance of the difference.