Not Quite the James-Stein Estimator

Review of Bias, Variance and MSE

The concepts of bias and variance are key ideas that we typically reach for when considering the quality of an estimator. To refresh your memory, bias is the difference between an estimators expected value and the true value of the parameter being estimated while variance is the expected squared difference between an estimator and its expected value. So if \(\hat{\theta}\) is an estimator of some unknown parameter \(\theta\), then \(\text{Bias}(\hat{\theta}) = \mathbb{E}[\hat{\theta}] - \theta\) while \(\text{Var}(\hat{\theta}) = \mathbb{E}[(\hat{\theta} - \mathbb{E}[\hat{\theta}])^2]\). A bias of zero means that an estimator is correctly centered: its expectation equals the truth. We say that such an estimator is unbiased.² A small variance means that an estimator is precise: it doesn’t “jump around” too much. Ideally we’d like an estimator that is correctly centered and precise. But it turns out that there is generally a trade-off between bias and variance: if you want to reduce one of them, you have to accept an increase in the other.

A common way of trading off bias and variance relies on a concept called mean-squared error (MSE) defined as the sum of the squared bias and the variance.³ In particular: \(\text{MSE}(\hat{\theta}) = \text{Var}(\hat{\theta}) + \text{Bias}(\hat{\theta})^2\). Equivalently, we can write \(\text{MSE}(\hat{\theta}) = \mathbb{E}[(\hat{\theta} - \theta)^2]\).⁴ To borrow some terminology from introductory microeconomics, you can think of MSE as the negative of a utility function over bias and variance. Both bias and variance are “bads” in that we’d rather have less rather than more of each. This formula expresses our preferences in terms of how much of one we’d be willing to accept in exchange for less of the other. Slightly foreshadowing something that will come later in this post, we can think of MSE as the square of the average distance that an archer’s arrows land from the bulls-eye. Smaller values of MSE are better: variance measures how closely the arrows cluster together while bias measures how far the center of the cluster is from the bulls-eye, as in the following diagram:

A Shrinkage Estimator

Returning to our maximum likelihood estimator: it’s unbiased, \(\text{Bias}(\hat{\mu}_{\text{ML}}) = 0\), so \(\text{MSE}(\hat{\mu}_{\text{ML}}) = \text{Var}(\hat{\mu}_{\text{ML}}) = 1\). Suppose that low MSE is what we’re after. Is there any way to improve on the ML estimator? In other words, can we achieve an MSE that’s lower than one? The answer turns out to be yes. Here’s the idea. Suppose we had some reason to believe that the true mean \(\mu\) isn’t very large. Then perhaps we could try to adjust our maximum likelihood estimate by shrinking slightly towards zero. One way to do this would be by taking a weighted average of the ML estimator and zero: \[ \hat{\mu}(\lambda) = (1 - \lambda) \times \hat{\mu}_{\text{ML}} + \lambda \times 0 = (1 - \lambda)X \] for \(0 \leq \lambda \leq 1\). The constant \((1 - \lambda)\) is called the “shrinkage factor” and controls how the ML estimator gets pulled towards zero.⁵ We get a different estimator for every value of \(\lambda\). If \(\lambda = 0\) then we get the ML estimator back. If \(\lambda = 1\) then we get a very silly estimator that ignores the data and simply reports zero no matter what! So let’s see how the MSE depends on our choice of \(\lambda\). Substituting the definition of \(\hat{\mu}(\lambda)\) into the formulas for bias and variance gives: \[ \begin{align*} \text{Bias}[\hat{\mu}(\lambda)]&= \mathbb{E}[(1 - \lambda)\hat{\mu}_\text{ML}] - \mu = (1 - \lambda)\mathbb{E}[\hat{\mu}_\text{ML}] - \mu = (1 - \lambda)\mu - \mu = -\lambda\mu\\ \\ \text{Var}[\hat{\mu}(\lambda)]&= \text{Var}[(1 - \lambda)\hat{\mu}_\text{ML}] = (1 - \lambda)^2\text{Var}[\hat{\mu}_\text{ML}] = (1 - \lambda)^2\\ \\ \text{MSE}[\hat{\mu}(\lambda)]&= \text{Var}[\hat{\mu}(\lambda)] + \text{Bias}[\hat{\mu}(\lambda)]^2 = (1 - \lambda)^2 + \lambda^2\mu^2 \end{align*} \] Unless \(\lambda = 0\), the shrinkage estimator is biased. And while the MSE of the ML estimator is always one, regardless of the true value of \(\mu\), the MSE of the shrinkage estimator depends on the unknown parameter \(\mu\).

So why should we use a biased estimator? The answer is that by tolerating a small amount of bias we may be able to achieve a larger reduction in variance, resulting in a lower MSE compared to the higher variance but unbiased ML estimator. A quick plot shows us that the shrinkage estimator can indeed have a lower MSE than the ML estimator depending on the value of \(\lambda\) and the true value of \(\mu\):

# Range of values for the unknown parameter mu
mu <- seq(-4, 4, length = 100)
# Try three different values of lambda
lambda1 <- 0.1
lambda2 <- 0.2
lambda3 <- 0.3
# Plot the MSE of the shrinkage estimator as a function of mu for all 
# three values of lambda at once
matplot(mu, cbind((1 - lambda1)^2 + lambda1^2 * mu^2, 
                  (1 - lambda2)^2 + lambda2^2 * mu^2, 
                  (1 - lambda3)^2 + lambda3^2 * mu^2), 
        type = 'l', lty = 1, lwd = 2, 
        col = c('red', 'blue', 'green'), 
        xlab = expression(mu), ylab = 'MSE', 
        main = 'MSE of Shrinkage Estimator')
# Add legend
legend('topright', legend = c(expression(lambda == 0.1), 
                              expression(lambda == 0.2), 
                              expression(lambda == 0.3)), 
       col = c('red', 'blue', 'green'), lty = 1, lwd = 2)
# Add dashed line for MSE of ML estimator
abline(h = 1, lty = 2, lwd = 2)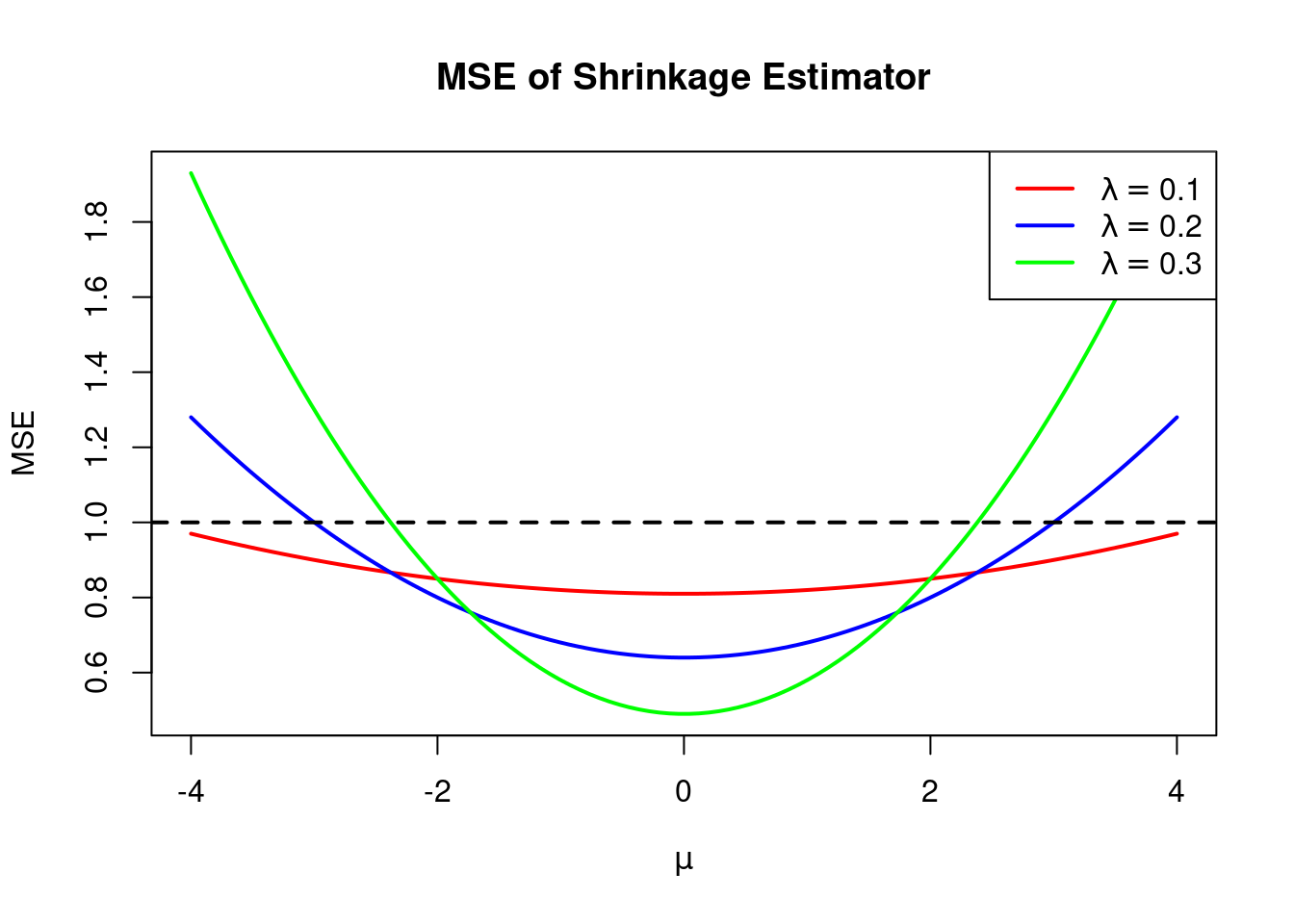

Some Algebra

It’s time for some algebra. If you’re tempted to skip this please don’t: this section is a warm-up for our main event. If you thoroughly understand the mechanics of shrinkage in this simple example, everything that follows below will seem much more natural.

As seen from the plot above, the MSE of our shrinkage estimator (the solid lines) is lower than that of the ML estimator (the dashed line) provided that our chosen value of \(\lambda\) isn’t too large relative to the true value of \(\mu\). With a bit of algebra, we can work out precisely how large \(\lambda\) can be to make shrinkage worthwhile. Since \(\text{MSE}[\hat{\mu}_\text{ML}]= 1\), by expanding and simplifying the expression for \(\text{MSE}[\hat{\mu}(\lambda)]\) we see that \(\text{MSE}[\hat{\mu}(\lambda)] < \text{MSE}[\hat{\mu}_\text{ML}]\) if and only if \[ \begin{align*} (1 - \lambda)^2 + \lambda^2\mu^2 &< 1 \\ 1 - 2\lambda + \lambda^2 + \lambda^2\mu^2 &< 1 \\ \lambda^2 (1 + \mu^2) -2 \lambda &< 0 \\ \lambda [\lambda (1 + \mu^2) - 2] &< 0. \end{align*} \] Since \(\lambda \geq 0\), the final inequality can only hold if the factor inside the square brackets is negative, i.e.  \[ \begin{align*} \lambda (1 + \mu^2) - 2 &< 0 \\ \lambda &< \frac{2}{1 + \mu^2}. \end{align*} \] This shows that any choice of \(\lambda\) between \(0\) and \(2 / (1 + \mu^2)\) will give us a shrinkage estimator with an MSE less than one. To check our algebra, we can change the inequality to an equality and solve for \(\mu\) to obtain the boundary of the region where shrinkage is better than ML: \[ \begin{align*} \lambda (1 + \mu^2) - 2 &= 0 \\ 1 + \mu^2 &= 2/\lambda \\ \mu &= \pm \sqrt{2/\lambda - 1}. \end{align*} \] Adding these boundaries to a simplified version of our previous plot with only \(\lambda = 0.3\) we see that everything works out correctly: the dashed red lines intersect the blue curve at the points where the MSE of the shrinkage estimator equals that of the ML estimator.

# Plot the MSE of the shrinkage estimator as a function of mu for lambda = 0.3
lambda <- 0.3
plot(mu, (1 - lambda)^2 + lambda^2 * mu^2, type = 'l', lty = 1, lwd = 2, 
     col = 'blue', xlab = expression(mu), ylab = 'MSE', 
     main = 'Boundary of Region Where Shrinkage is Better than ML')
# Add dashed line for MSE of ML estimator
abline(h = 1, lty = 2, lwd = 2)
# Add boundaries of region where shrinkage is better than ML estimator
abline(v = c(sqrt(2/lambda - 1), -sqrt(2/lambda - 1)), lty = 3, lwd = 2,
       col = 'red')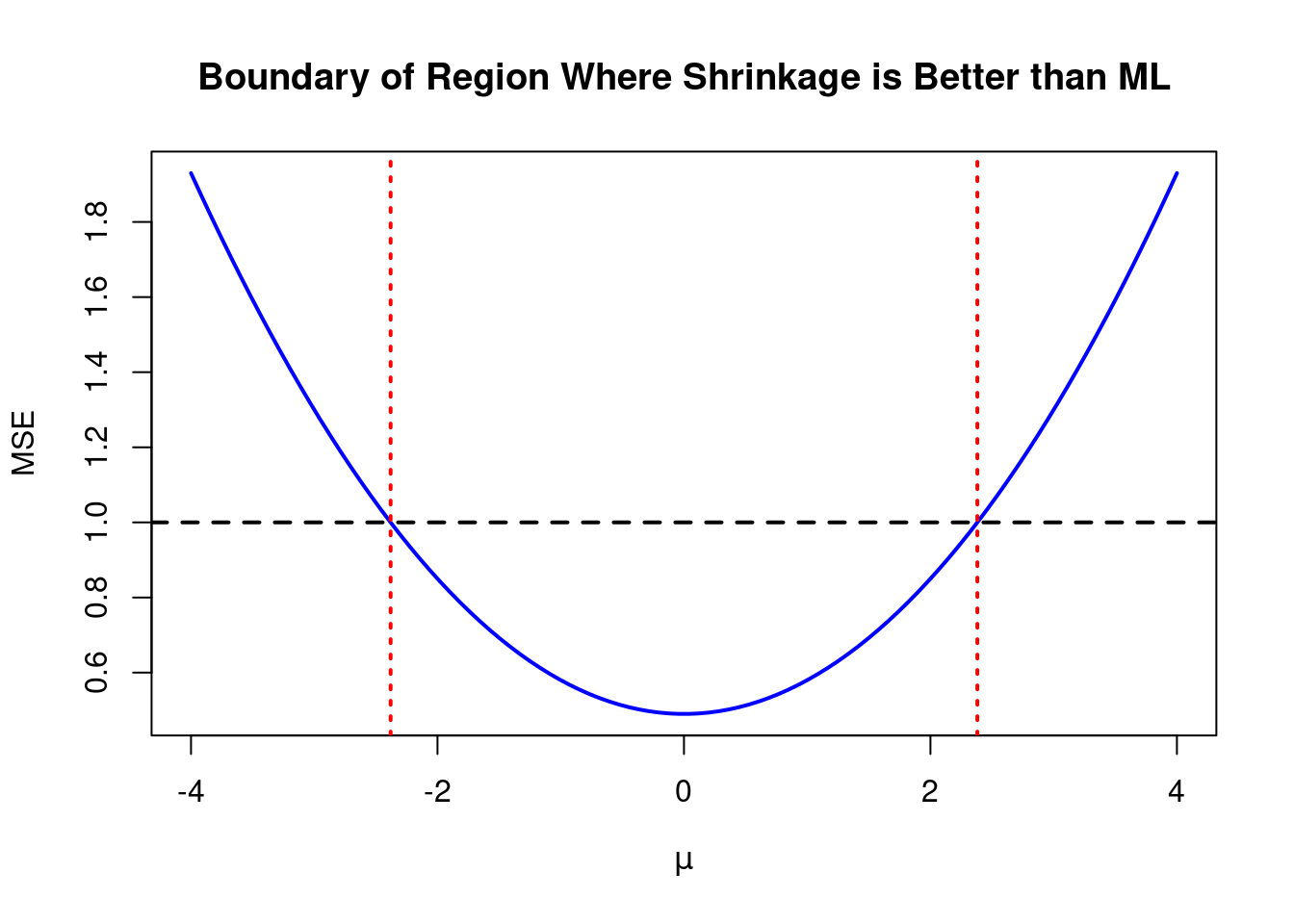

But there’s still more to learn! Suppose we wanted to take things one step further and find the optimal value of \(\lambda\) for any given value of \(\mu\). In other words, suppose we wanted the value of \(\lambda\) that minimizes the MSE of our shrinkage estimator given a particular assumed value for \(\mu\). Since \(\text{MSE}[\hat{\mu}(\lambda)]\) is a quadratic function of \(\lambda\), as shown above, this turns out to be a fairly straightforward calculation. Differentiating, \[ \begin{align*} \frac{d}{d\lambda}\text{MSE}[\hat{\mu}(\lambda)] &= \frac{d}{d\lambda}[(1 - \lambda)^2 + \lambda^2 \mu^2] \\ &= -2(1 - \lambda) + 2\lambda \mu^2 \\ &= 2 [\lambda (1 + \mu^2) - 1]\\ \\ \frac{d^2}{d\lambda^2}\text{MSE}[\hat{\mu}(\lambda)] &= 2(1 + \mu^2) > 0 \end{align*} \] so there is a unique global minimum at \(\lambda^* \equiv 1/(1 + \mu^2)\). This gives the optimal shrinkage factor in the sense that it minimizes the MSE of the shrinkage estimator. Substituting \(\lambda^*\) into the expression for \(\text{MSE}[\hat{\mu}(\lambda)]\) gives: \[ \begin{align*} \text{MSE}[\hat{\mu}(\lambda^*)] &= \left(1 - \frac{1}{1 + \mu^2} \right)^2 + \left(\frac{1}{1 + \mu^2}\right)^2 \mu^2 \\ &= \left( \frac{\mu^2}{1 + \mu^2}\right)^2 + \left(\frac{1}{1 + \mu^2}\right)^2 \mu^2 \\ &= \left( \frac{1}{1 + \mu^2}\right)^2 (\mu^4 + \mu^2) \\ &= \left( \frac{1}{1 + \mu^2}\right)^2 \mu^2(1 + \mu^2) \\ &= \frac{\mu^2}{1 + \mu^2} < 1. \end{align*} \]

Recap

We’re moments away from having all the ingredients we need to introduce Stein’s Paradox! But first let’s review what we’ve uncovered thus far. We’ve seen that the shrinkage estimator can improve on the ML estimator in terms of MSE provided that \(\lambda\) is chosen judiciously: it needs to be between zero and \(2/(1 + \mu^2)\). The optimal choice of \(\lambda\), namely \(\lambda^* = 1 / (1 + \mu^2)\), gives an MSE of \(\mu^2/(1 + \mu^2)\). This is always lower than one, the MSE of the ML estimator.

There’s just one massive problem we’ve ignored this whole time: we don’t know the value of \(\mu\)! As seen from the figure plotted above, the MSE curves for different values of \(\lambda\) cross each other: the best one to use depends on the true value of \(\mu\). This doesn’t mean that all is lost. Perhaps in practice we have some outside information about the likely value of \(\mu\) that could help guide our choice of \(\lambda\). What it does mean is that there’s no “one-size-fits-all” value.

Admissibility

It’s time to introduce a bit of technical vocabulary. We say that an estimator \(\tilde{\theta}\) dominates another estimator \(\hat{\theta}\) if \(\text{MSE}[\tilde{\theta}] \leq \text{MSE}[\hat{\theta}]\) for all possible values of the parameter \(\theta\) being estimated and \(\text{MSE}[\tilde{\theta}] < \text{MSE}[\hat{\theta}]\) for at least one possible value of \(\theta\).⁶ In words, this means that it never makes sense to use \(\hat{\theta}\) in preference to \(\tilde{\theta}\). No matter what the true parameter value is, you can’t do worse with \(\tilde{\theta}\) and you might do better. An estimator that is not dominated by any other estimator is called admissible; an estimator that is dominated by some other estimator is called inadmissible. The concept of admissibility in decision theory is a bit like the concept of Pareto efficiency in microeconomics. An admissible estimator is only “good” in the sense that it doesn’t leave any money on the table: there’s no way to do better for one parameter value without doing worse for another. In a similar way, a Pareto efficient allocation in economics is one in which no individual can be made better off without making another person worse off.

It’s quite challenging to prove, but in fact the ML estimator \(\hat{\theta}_{ML} = X\) turns out to be admissible in our little example. So while we could potentially do better by using shrinkage, it’s not a slam-dunk case. If we really have no idea of how large \(\mu\) is likely to be, the ML estimator is a reasonable choice. Because it’s admissible, at the very least we know that there’s no free lunch!

A More General Example

Now let’s make things a bit more interesting. For the rest of this post, suppose that we observe not a single draw \(X\) from a \(\text{Normal}(\mu, 1)\) distribution but a collection of \(p\) independent draws from \(p\) different normal distributions: \[ X_1, X_2, ..., X_p \sim \text{independent Normal}(\mu_j, 1), \quad j = 1, ..., p. \] You can think of this as \(p\) copies of our original problem: we observe \(X_j \sim \text{Normal}(\mu_j, 1)\) and our task is to estimate \(\mu_j\). The observations are all independent, and each comes from a distribution with a potentially different mean. At first glance it seems like these \(p\) separate problems should have absolutely nothing to do with each other. And indeed the maximum likelihood estimator for the collection of \(p\) means is simply \(\hat{\mu}^{(j)}_\text{ML} = X_j\). As above in our example with \(p=1\), the question is: how good is the ML estimator, and can we do any better?

Composite MSE

But first things first: how can we evaluate the quality of \(p\) estimators for \(p\) different parameters at the same time? A common approach, and the one we will follow here, is to take the sum of the individual MSEs of each estimator, yielding a quantity called composite MSE. If \(\hat{\mu}_1, \hat{\mu}_2, \dots, \hat{\mu}_p\) is a collection of estimators for each of the individual unknown means, then the composite MSE is defined as \[ \text{Composite MSE} \equiv \sum_{j=1}^p \text{MSE}(\hat{\mu}_j) = \sum_{j=1}^p \left[ \text{Bias}(\hat{\mu}_j)^2 + \text{Var}(\hat{\mu}_j)\right] = \sum_{j=1}^p \mathbb{E}[(\hat{\mu}_j - \mu_j)^2]. \] Adopting composite MSE as our measure of good performance means that we view each of the \(p\) estimation problems as in some way “interchangeable”–we’re happy to accept a trade in which we do a slightly worse job estimating \(\mu_j\) in exchange for doing a much better job estimating \(\mu_k\). At the end of the post I’ll say a few more words about this idea and when it may or may not be reasonable. But for the rest of the post, we will assume that our goal is to minimize the composite MSE. The concept of composite MSE will be crucial in understanding why the James-Stein estimator works the way it does.

Stein’s Paradox

Putting our new idea into practice, we see that the composite MSE of the ML estimator is \(p\) regardless of the true values of the individual means \(\mu_1, \dots, \mu_p\) since \[ \sum_{j=1}^p \text{MSE}\left[\hat{\mu}^{(j)}_\text{ML}\right] = \sum_{j=1}^p \text{MSE}(X_j) = \sum_{j=1}^p \text{Var}(X_j) = p. \] If the ML estimator is admissible, then there should be no other estimator that always has an MSE less than or equal to \(p\) and sometimes has an MSE strictly less than \(p\). I’ve already told you that this is true when \(p = 1\). When \(p = 2\) it’s still true: the ML estimator remains admissible. But when \(p \geq 3\) something very unexpected happens: it becomes possible to construct an estimator that dominates the ML estimator by using information from all of the \((X_1, ..., X_p)\) observations to estimate \(\mu_j\). This is spite of the fact that there is no obvious connection between the observations. Again: they are all independent and come from distributions with different means!

The estimator that does the trick is the so-called “James-Stein Estimator” (JS), defined according to \[ \hat{\mu}^{(j)}_\text{JS} = \left(1 - \frac{p - 2}{\sum_{k=1}^p X_k^2}\right)X_j. \] This this estimator dominates the ML estimator when \(p \geq 3\) in that
\[ \sum_{j=1}^p \text{MSE}\left[\hat{\mu}^{(j)}_\text{JS}\right] \leq \sum_{j=1}^p \text{MSE}\left[\hat{\mu}^{(j)}_\text{ML}\right]= p \] for all possible values of the \(p\) unknown means \(\mu_j\) with strict inequality for at least some values. Taking a closer look at the formula, we see that the James-Stein estimator is just a shrinkage estimator applied to each of the \(p\) means, namely \[ \hat{\mu}^{(j)}_\text{JS} = (1 - \hat{\lambda}_\text{JS})X_j, \quad \hat{\lambda}_\text{JS} \equiv \frac{p - 2}{\sum_{k=1}^p X_k^2}. \] The shrinkage factor in the James-Stein estimator depends on the number of means we’re estimating, \(p\), along with the overall sum of the squared observations. All else equal, the more parameters we need to estimate, the more we shrink each of them towards zero. And the farther the observations are from zero overall, the less we shrink each of them towards zero.

Just like our simple shrinkage estimator from above, the James-Stein estimator achieves a lower MSE by tolerating a small bias in exchange for a larger reduction in variance, compared to the higher-variance but unbiased ML estimator. Unlike our simple shrinkage estimator, the James-Stein estimator uses the data to determine the shrinkage factor. And as long as \(p\leq 3\) it is always at least as good as the ML estimator and sometimes much better. The paradox is that this seems impossible: how can information from all of the observations be useful when they come from different distributions with no obvious connection?

The rest of this post will not prove that the James-Stein estimator dominates the ML estimator. Instead it will try to convince you that there is some very good intuition for why the formula for the James-Stein estimator. By the end, I hope you’ll feel that, far from seeming paradoxical, using all of the observations to determine the shrinkage factor for one particular \(\mu_j\) makes perfect sense.

An Infeasible Estimator When \(p = 2\)

To start the ball rolling, let’s assume a can-opener: suppose that we don’t know any of the individual means \(\mu_j\) but for some strange reason a benevolent deity has told us the value of their sum of squares: \[ c^2 \equiv \sum_{j=1}^p \mu_j^2 \equiv c^2. \] It turns out that this is enough information to construct a shrinkage estimator that always has a lower composite MSE than the ML estimator. Let’s see why this is the case. If \(p = 1\), then telling you \(c^2\) is the same as telling you \(\mu^2\). Granted, knowledge of \(\mu^2\) isn’t as informative as knowledge of \(\mu\). For example, if I told you that \(\mu^2 = 9\) you couldn’t tell whether \(\mu = 3\) or \(\mu = -3\). But, as we showed above, the optimal shrinkage estimator when \(p=1\) sets \(\lambda^* = 1/(1 + \mu^2)\) and yields an MSE of \(\mu^2/(1 + \mu^2) < 1\). Since \(\lambda^*\) only depends on \(\mu\) through \(\mu^2\), we’ve already shown that knowledge of \(c^2\) allows us to construct a shrinkage estimator that dominates the ML estimator when \(p = 1\).

So what if \(p\) equals 2? In this case, knowledge of \(c^2 = \mu_1^2 + \mu_2^2\) is equivalent to knowing the radius of a circle centered at the origin in the \((\mu_1, \mu_2)\) plane where the two unknown means must lie. For example, if I told you that \(c^2 = 1\) you would know that \((\mu_1, \mu_2)\) lies somewhere on a circle of radius one centered at the origin. As illustrated in the following plot, the points \((x_1, x_2)\) and \((y_1, y_2)\) would then be potential values of \((\mu_1, \mu_2)\) as would all other points on the blue circle.

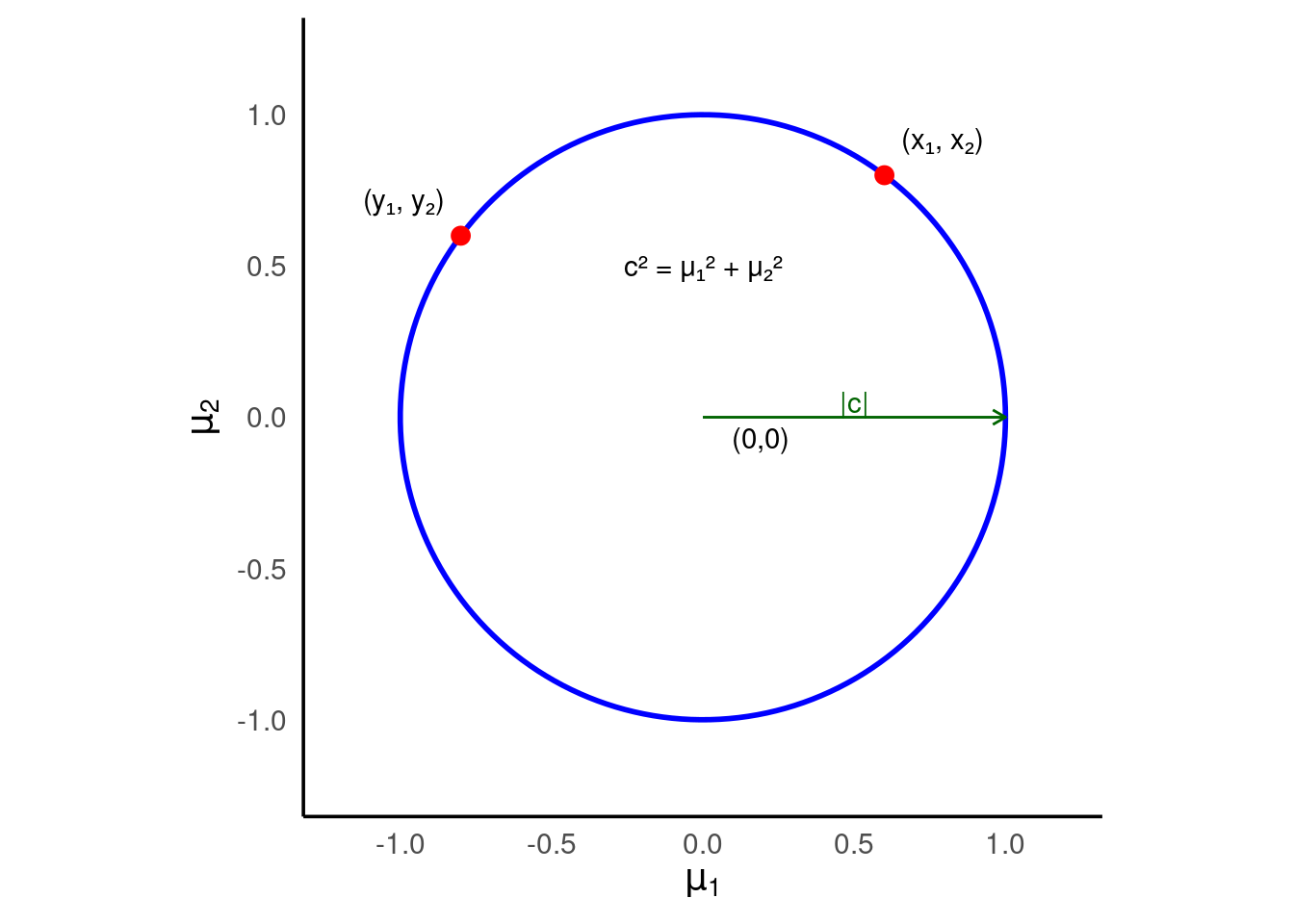
So how can we construct a shrinkage estimator of \((\mu_1, \mu_2)\) with lower composite MSE than the ML estimator if \(c^2\) is known? While there are other possibilities, the simplest would be to use the same shrinkage factor for each of the two coordinates. In other words, our estimator would be \[ \hat{\mu}_1(\lambda) = (1 - \lambda)X_1, \quad \hat{\mu}_2(\lambda) = (1 - \lambda)X_2 \] for some \(\lambda\) between zero and one. The composite MSE of this estimator is just the sum of the MSE of each individual component, so we can re-use our algebra from above to obtain \[ \begin{align*} \text{MSE}[\hat{\mu}_1(\lambda)] + \text{MSE}[\hat{\mu}_2(\lambda)] &= [(1 - \lambda)^2 + \lambda^2\mu_1^2] + [(1 - \lambda)^2 + \lambda^2\mu_2^2] \\ &= 2(1 - \lambda)^2 + \lambda^2(\mu_1^2 + \mu_2^2) \\ &= 2(1 - \lambda)^2 + \lambda^2c^2. \end{align*} \] Notice that the composite MSE only depends on \((\mu_1, \mu_2)\) through their sum of squares, \(c^2\). Differentiating with respect to \(\lambda\), just as we did above in the \(p=1\) case, \[ \begin{align*} \frac{d}{d\lambda}\left[2(1 - \lambda)^2 + \lambda^2c^2\right] &= -4(1 - \lambda) + 2\lambda c^2 \\ &= 2 \left[\lambda (2 + c^2) - 2\right]\\ \\ \frac{d^2}{d\lambda^2}\left[2(1 - \lambda)^2 + \lambda^2c^2\right] &= 2(2 + c^2) > 0 \end{align*} \] so there is a unique global minimum at \(\lambda^* = 2/(2 + c^2)\). Substituting this value of \(\lambda\) into the expression for the composite MSE, a few lines of algebra give \[ \begin{align*} \text{MSE}[\hat{\mu}_1(\lambda^*)] + \text{MSE}[\hat{\mu}_2(\lambda^*)] &= 2\left(1 - \frac{2}{2 + c^2}\right)^2 + \left(\frac{2}{2 + c^2}\right)^2c^2 \\ &= 2\left(\frac{c^2}{2 + c^2}\right). \end{align*} \] Since \(c^2/(2 + c^2) < 1\) for all \(c^2 > 0\), the optimal shrinkage estimator always has a composite MSE lower less than \(2\), the composite MSE of the ML estimator. Strictly speaking this estimator is infeasible since we don’t know \(c^2\). But it’s a crucial step on our journal to make the leap from applying shrinkage to an estimator for a single unknown mean, to using the same idea for more than one uknown mean.

A Simulation Experiment for \(p = 2\)

You may have already noticed that it’s easy to generalize this argument to \(p>2\). But before we consider the general case, let’s take a moment to understand the geometry of shrinkage estimation for \(p=2\) a bit more deeply. The nice thing about two-dimensional problems is that they’re easy to plot. So here’s a graphical representation of both the ML estimator and our infeasible optimum shrinkage estimator when \(p = 2\). I’ve set the true, unknown, values of \(\mu_1\) and \(\mu_2\) to one so the true value of \(c^2\) is \(2\) and the optimal choice of \(\lambda\) is \(\lambda^* = 2/(2 + c^2) = 2/4 = 0.5\). The following R code simulates our estimators and visualizes their performance, helping us see the shrinkage effect in action.

set.seed(1983)

nreps <- 50
mu1 <- mu2 <- 1
x1 <- mu1 + rnorm(nreps)
x2 <- mu2 + rnorm(nreps)

csq <- mu1^2 + mu2^2
lambda <- csq / (2 + csq)

par(mfrow = c(1, 2))

# Left panel: ML Estimator
plot(x1, x2, main = 'MLE', pch = 20, col = 'black', cex = 2, 
     xlab = expression(mu[1]), ylab = expression(mu[2]))
abline(v = mu1, lty = 1, col = 'red', lwd = 2)
abline(h = mu2, lty = 1, col = 'red', lwd = 2)

# Add MSE to the plot
text(x = 2, y = 3, labels = paste("MSE =", 
                                  round(mean((x1 - mu1)^2 + (x2 - mu2)^2), 2)))

# Right panel: Shrinkage Estimator
plot(x1, x2, main = 'Shrinkage', xlab = expression(mu[1]), 
     ylab = expression(mu[2]))
points(lambda * x1, lambda * x2, pch = 20, col = 'blue', cex = 2)
segments(x0 = x1, y0 = x2, x1 = lambda * x1, y1 = lambda * x2, lty = 2)
abline(v = mu1, lty = 1, col = 'red', lwd = 2)
abline(h = mu2, lty = 1, col = 'red', lwd = 2)
abline(v = 0, lty = 1, lwd = 2)
abline(h = 0, lty = 1, lwd = 2)

# Add MSE to the plot
text(x = 2, y = 3, labels = paste("MSE =", 
                                  round(mean((lambda * x1 - mu1)^2 + 
                                               (lambda * x2 - mu2)^2), 2)))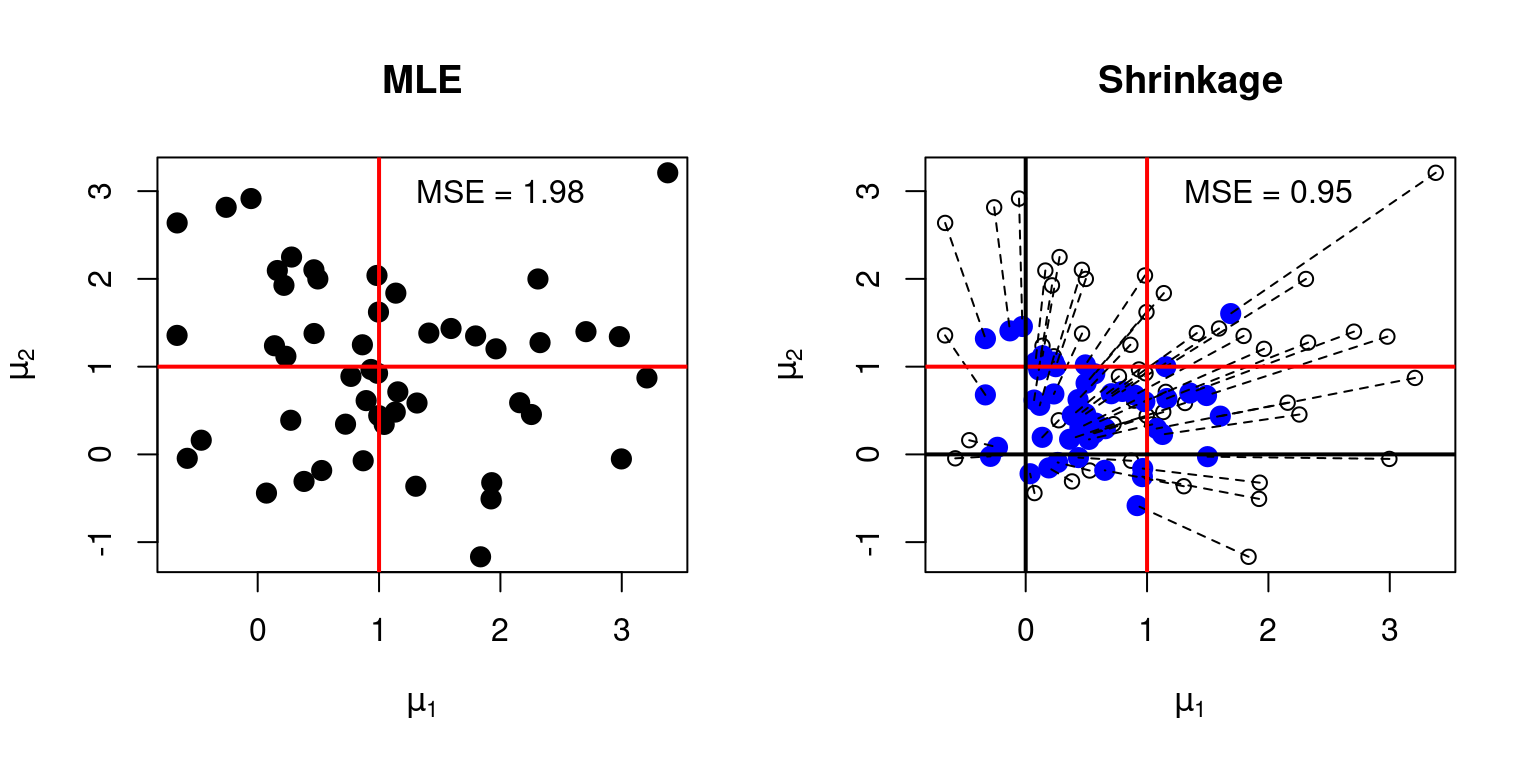

My plot has two panels. The left panel shows the raw data. Each black point is a pair \((X_1, X_2)\) of independent normal draws with means \((\mu_1 = 1, \mu_2 = 1)\) and variances \((1, 1)\). As such, each point is also the ML estimate (MLE) of \((\mu_1, \mu_2)\) based on \((X_1, X_2)\). The red cross shows the location of the true values of \((\mu_1, \mu_2)\), namely \((1, 1)\). There are 50 points in the plot, representing 50 replications of the simulation, each independent of the rest and with the same parameter values. This allows us to measure how close the ML estimator is to the true value of \((\mu_1, \mu_2)\) in repeated sampling, approximating the composite MSE.

The right panel is more complicated. This shows both the ML estimates (unfilled black circles) and the corresponding shrinkage estimates (filled blue circles) along with dashed lines connecting them. Each shrinkage estimate is constructed by “pulling” the corresponding MLE towards the origin by a factor of \(\lambda = 0.5\). Thus, if a given unfilled black circle is located at \((X_1, X_2)\), the corresponding filled blue circle is located at \((0.5X_1, 0.5X_2)\). As in the left panel, the red cross in the right panel shows the true values of \((\mu_1, \mu_2)\), namely \((1, 1)\). The black cross, on the other hand, shows the point towards which the shrinkage estimator pulls the ML estimator, namely \((0, 0)\).

We see immediately that the ML estimator is unbiased: the black filled dots in the left panel (along with the unfilled ones in the right) are centered at \((1, 1)\). But the ML estimator is also high-variance: the black dots are quite spread out around \((1, 1)\). We can approximate the composite MSE of the ML estimator by computing the average squared Euclidean distance between the black points and the red cross.⁷ And in keeping with our theoretical calculations, the simulation gives a composite MSE of almost exactly 2 for the ML estimator.

In contrast, the optimal shrinkage estimator is biased: the filled blue dots in the right panel centered somewhere between the red cross (the true means) and the origin. But the shrinkage estimator also has a lower variance: the filled blue dots are much closer together than the black ones. Even more importantly they are on average closer to \((\mu_1, \mu_2)\), as indicated by the red cross and as measured by composite MSE. Our theoretical calculations showed that the composite MSE of the optimal shrinkage estimator equals \(2c^2/(2 + c^2)\). When \(c^2 = 2\), as in this case, we obtain \(2\times 2/(2 + 2) = 1\). Again, this is almost exactly what we see in the simulation.

If we had used more than 50 simulation replications, the composite MSE values would have been even closer to our theoretical predictions, at the cost of making the plot much harder to read! But I hope the key point is still clear: shrinkage pulls the MLE towards the origin, and can give a much lower composite MSE.

An Infeasible Estimator: The General Case

Now that we understand the case of \(p=2\), the general case is a snap. Our shrinkage estimator of each \(\mu_j\) will take the form \[ \hat{\mu}_j(\lambda) = (1 - \lambda) X_j, \quad j = 1, \dots, p \] for some \(\lambda\) between zero and one. To find the optimal choice of \(\lambda\), we minimize \[ \sum_{j=1}^p\text{MSE}\left[\hat{\mu}_j(\lambda) \right] = \sum_{j=1}^p \left[(1 - \lambda)^2 + \lambda^2 \mu_j^2\right] = p(1 - \lambda)^2 + \lambda^2 c^2 \] with respect to \(\lambda\). Again, the key is that the composite MSE only depends on the unknown means through \(c^2\). Using almost exactly the same calculations as above for the case of \(p = 2\), we find that \[ \lambda^* = \frac{p}{p + c^2}, \quad \sum_{j=1}^p \text{MSE}\left[\hat{\mu}_j(\lambda^*) \right] = p\left(\frac{c^2}{p + c^2}\right). \] since \(c^2/(p + c^2) < 1\) for all \(c^2 > 0\), the optimal shrinkage estimator always has a composite MSE less than \(p\), the composite MSE of the ML estimator.

Not Quite the James-Stein Estimator

The end is in sight! We’ve shown that if we knew the sum of squares of the unknown means, \(c^2\), we could construct a shrinkage estimator that always has a lower composite MSE than the ML estimator. But we don’t know \(c^2\). So what can we do? To start off, re-write \(\lambda^*\) as follows \[ \lambda^* = \frac{p}{p + c^2} = \frac{1}{1 + c^2/p}. \] This way of writing things makes it clear that it’s not \(c^2\) per se that matters but rather \(c^2/p\). And this quantity is simply is the average of the unknown squared means: \[ \frac{c^2}{p} = \frac{1}{p}\sum_{j=1}^p \mu_j^2. \] So how could we learn \(c^2/p\)? An idea that immediately suggests itself is to estimate this quantity by replacing each unobserved \(\mu_j\) with the corresponding observation \(X_j\), in other words \[ \frac{1}{p}\sum_{j=1}^p X_j^2. \] This is a good starting point, but we can do better. Since \(X_j \sim \text{Normal}(\mu_j, 1)\), we see that \[ \mathbb{E}\left[\frac{1}{p} \sum_{j=1}^p X_j^2 \right] = \frac{1}{p} \sum_{j=1}^p \mathbb{E}[X_j^2] = \frac{1}{p} \sum_{j=1}^p [\text{Var}(X_j) + \mathbb{E}(X_j)^2] = \frac{1}{p} \sum_{j=1}^p (1 + \mu_j^2) = 1 + \frac{c^2}{p}. \] This means that \((\sum_{j=1}^p X_j^2)/p\) will on average overestimate \(c^2/p\) by one. But that’s a problem that’s easy to fix: simply subtract one! This is a rare situation in which there is no bias-variance tradeoff. Subtracting a constant, in this case one, doesn’t contribute any additional variation while completely removing the bias. Plugging into our formula for \(\lambda^*\), this suggests using the estimator \[ \hat{\lambda} \equiv \frac{1}{1 + \left[\left(\frac{1}{p}\sum_{j=1}^p X_j^2 \right) - 1\right]} = \frac{1}{\frac{1}{p}\sum_{j=1}^p X_j^2} = \frac{p}{\sum_{j=1}^p X_j^2} \] as our stand-in for the unknown \(\lambda^*\), yielding a shrinkage estimator that I’ll call “NQ” for “not quite” for reasons that will become apparent in a moment: \[ \hat{\mu}^{(j)}_\text{NQ} = \left(1 - \frac{p}{\sum_{k=1}^p X_k^2}\right)X_j. \] Notice what’s happening here: our optimal shrinkage estimator depends on \(c^2/p\), something we can’t observe. But we’ve constructed an unbiased estimator of this quantity by using all of the observations \(X_j\). This is the resolution of the paradox discussed above: all of the observations contain information about \(c^2\) since this is simply the sum of the squared means. And because we’ve chosen to minimize composite MSE, the optimal shrinkage factor only depends on the individual \(\mu_j\) parameters through \(c^2\)! This is the sense in which it’s possible to learn something useful about, say, \(\mu_1\) from \(X_2\) in spite of the fact that \(\mathbb{E}[X_2] = \mu_2\) may bear no relationship to \(\mu_1\).

But wait a minute! This looks suspiciously familiar. Recall that the James-Stein estimator is given by \[ \hat{\mu}^{(j)}_\text{JS} = \left(1 - \frac{p - 2}{\sum_{k=1}^p X_k^2}\right)X_j. \] Just like the JS estimator, my NQ estimator shrinks each of the \(p\) means towards zero by a factor that depends on the number of means we’re estimating, \(p\), and the overall sum of the squared observations. The key difference between JS and NQ is that JS uses \(p - 2\) in the numerator instead of \(p\). This means that NQ is a more “aggressive” shrinkage estimator than JS: it pulls the means towards zero by a larger amount than JS. This difference turns out to be crucial for proving that the JS estimator dominates the ML estimator. But when it comes to understanding why the JS estimator has the form that it does, I would argue that the difference is minor. If you want all the gory details of where that extra \(-2\) comes from, along with the closely related issue of why \(p\geq 3\) is crucial for JS to dominate the ML estimator, see lecture 1 or section 7.3 from my Econ 722 teaching materials.