Econometrics Puzzler #2: Fitting a Regression with Fitted Values

Example: Height and Handspan

Here’s a simple example: a regression of height, measured in inches, on handspan, measured in centimeters.¹

library(tidyverse)
library(broom)
dat <- read_csv('https://ditraglia.com/data/height-handspan.csv')

ggplot(dat, aes(y = height, x = handspan)) +
  geom_point(alpha = 0.2) +
  geom_smooth(method = "lm", color = "red") +
  labs(y = "Height (in)", x = "Handspan (cm)")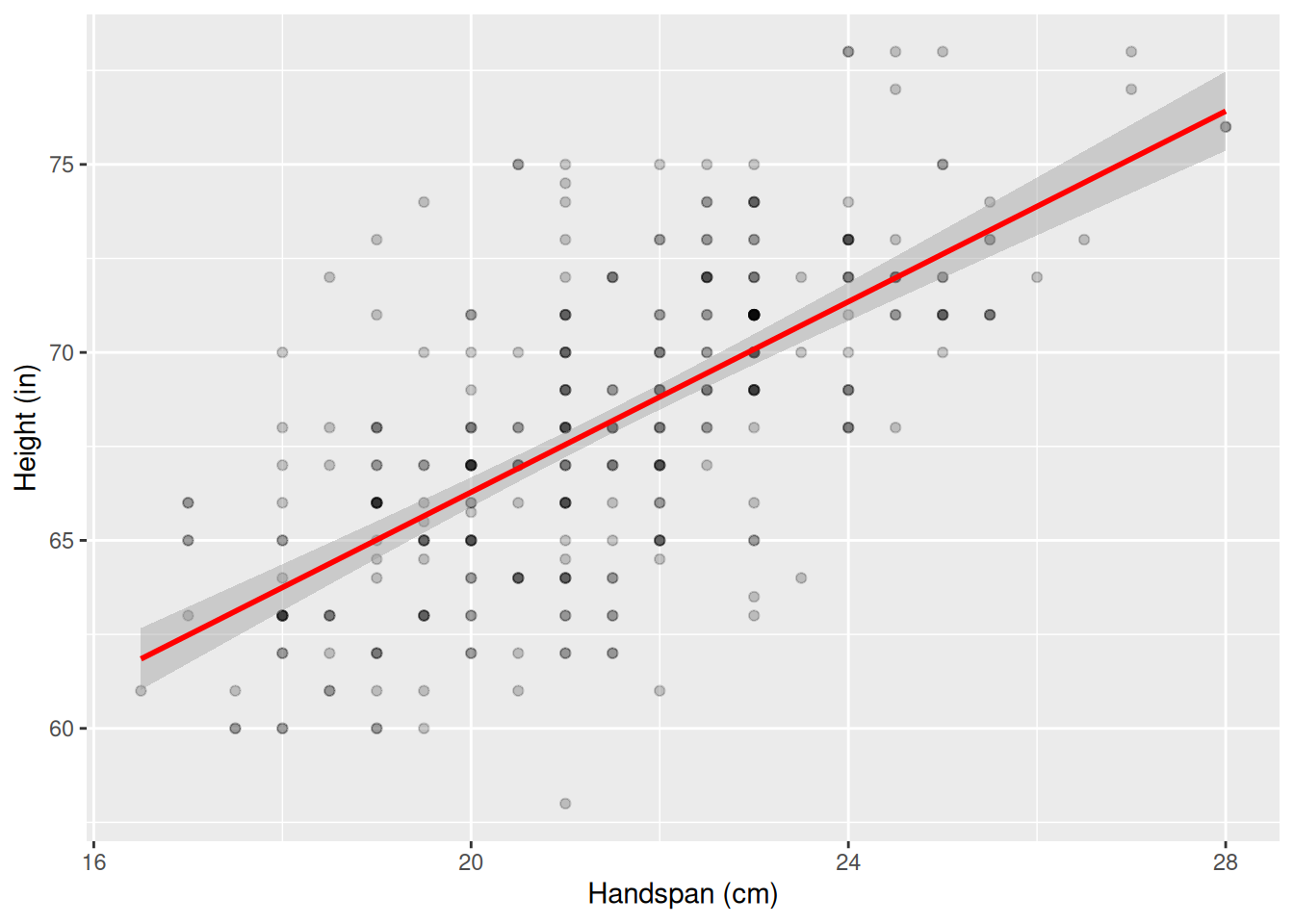

# Fit the regression
reg1 <- lm(height ~ handspan, data = dat)
tidy(reg1)

## # A tibble: 2 × 5
##   term        estimate std.error statistic  p.value
##   <chr>          <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)    40.9     1.67        24.5 9.19e-76
## 2 handspan        1.27    0.0775      16.3 3.37e-44

As expected, bigger people are bigger in all dimensions, on average, so we see a positive relationship between handspan and height. Now let’s save the fitted values from this regression and run a second regression of height on the fitted values:

dat <- reg1 |> 
  augment(dat)
reg2 <- lm(height ~ .fitted, data = dat)
tidy(reg2)

## # A tibble: 2 × 5
##   term         estimate std.error statistic   p.value
##   <chr>           <dbl>     <dbl>     <dbl>     <dbl>
## 1 (Intercept) -1.76e-13    4.17   -4.23e-14 1.000e+ 0
## 2 .fitted      1.00e+ 0    0.0612  1.63e+ 1 3.37 e-44

The intercept isn’t quite zero, but it’s about as close as we can reasonably expect to get on a computer and the slope is exactly one. Now how about the R-squared? Let’s check:

glance(reg1)

## # A tibble: 1 × 12
##   r.squared adj.r.squared sigma statistic  p.value    df logLik   AIC   BIC
##       <dbl>         <dbl> <dbl>     <dbl>    <dbl> <dbl>  <dbl> <dbl> <dbl>
## 1     0.452         0.450  3.02      267. 3.37e-44     1  -822. 1650. 1661.
## # ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>

glance(reg2)

## # A tibble: 1 × 12
##   r.squared adj.r.squared sigma statistic  p.value    df logLik   AIC   BIC
##       <dbl>         <dbl> <dbl>     <dbl>    <dbl> <dbl>  <dbl> <dbl> <dbl>
## 1     0.452         0.450  3.02      267. 3.37e-44     1  -822. 1650. 1661.
## # ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>

The R-squared values from the two regressions are identical! Surprised? Now’s your last chance to think it through on your own before I give my solution.

Solution

Suppose we wanted to choose \(\alpha_0\) and \(\alpha_1\) to minimize \(\sum_{i=1}^n (Y_i - \alpha_0 - \alpha_1 \widehat{Y}_i)^2\) where \(\widehat{Y}_i = \widehat{\beta}_0 + \widehat{\beta}_1 X_i\). This is equivalent to minimizing \[ \sum_{i=1}^n \left[Y_i - (\alpha_0 + \alpha_1 \widehat{\beta}_0) - (\alpha_1\widehat{\beta}_1)X_i\right]^2. \] By construction \(\widehat{\beta}_0\) and \(\widehat{\beta}_1\) minimize \(\sum_{i=1}^n (Y_i - \beta_0 - \beta_1 X_i)^2\), so unless \(\widehat{\alpha_0} = 0\) and \(\widehat{\alpha_1} = 1\) we’d have a contradiction!

Similar reasoning explains why the R-squared values for the two regressions are the same. The R-squared of a regression equals \(1 - \text{SS}_{\text{residual}} / \text{SS}_{\text{total}}\) \[ \text{SS}_{\text{total}} = \sum_{i=1}^n (Y_i - \bar{Y})^2,\quad \text{SS}_{\text{residual}} = \sum_{i=1}^n (Y_i - \widehat{Y}_i)^2 \] The total sum of squares is the same for both regressions because they have the same outcome variable. The residual sum of squares is the same because \(\widehat{\alpha}_0 = 0\) and \(\widehat{\alpha}_1 = 1\) together imply that both regressions have the same fitted values.

Here I focused on the case of a simple linear regression, one with a single predictor variable, but the same basic idea holds in general.